excel-lambda-INTRATE.EFFECTIVE – calculate effective interest rate in Excel without iterative calculation

The gist for this lambda can be found here.

The goal

I saw a video from Diarmuid Early in which he discusses the use of the iterative calculation setting in Excel for calculating effective interest rates. 

I share a similar view that using that setting can be very dangerous and if possible, it’s best to avoid it.

So:

Create a simple recursive lambda function that can be used to converge on an effective interest rate (i.e. that includes “interest on the interest”)

I’d like to preface this post by saying that the lambda shown here is based on a very simple example as described at the beginning of the video linked above. The actual logic used in a model is likely to be far more complex than included here and so my intent is only to describe a strategy for recursion in a financial context, not to provide a bulletproof solution.

A solution

Here’s a lambda I’ve called INTRATE.EFFECTIVE:

=LAMBDA(opening_balance, base_rate, [interest],
    LET(
        _int, IF(ISOMITTED(interest), 0, interest),
        _new_close, opening_balance + _int,
        _avg_balance, AVERAGE(opening_balance, _new_close),
        _new_int, _avg_balance * base_rate,
        _effective_rate, IF(
            ROUND(_new_int, 2) = ROUND(_int, 2),
            _new_int / opening_balance,
            INTRATE.EFFECTIVE(opening_balance,base_rate,_new_int)
        ),
        _effective_rate
    )
)

The lambda allows three parameters, but when calling from the spreadsheet, we should only use the first two, as will become clear below:

1. opening_balance – the opening balance of some period of interest
2. base_rate – the base rate of the instrument
3. [interest] – OPTIONAL – this is used by the recursion to pass the calculated interest back into the formula to calculate the closing balance (and therefore average balance) during each iteration. Generally speaking, this should not be used when using this function to call from the downs 

Here’s how it works:

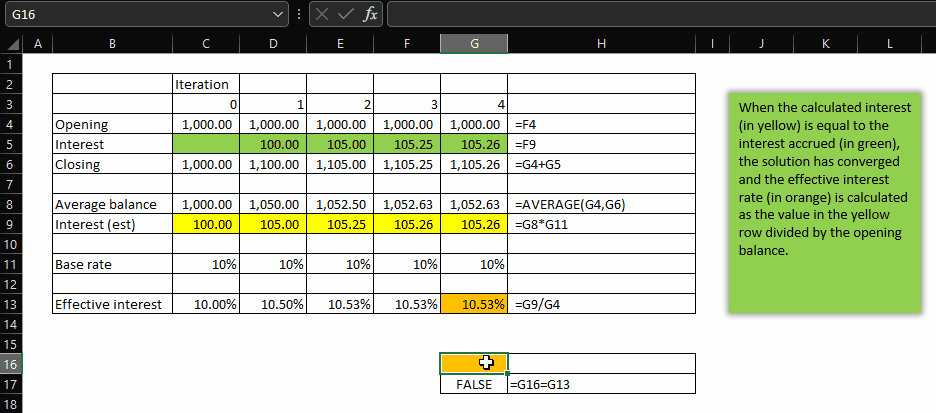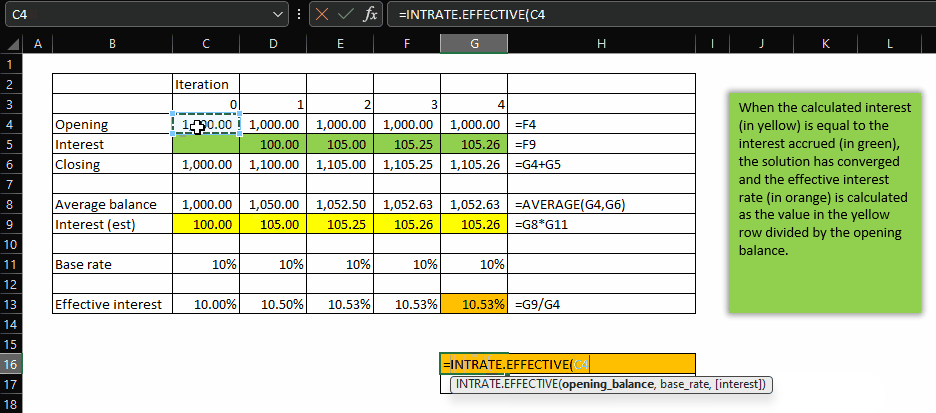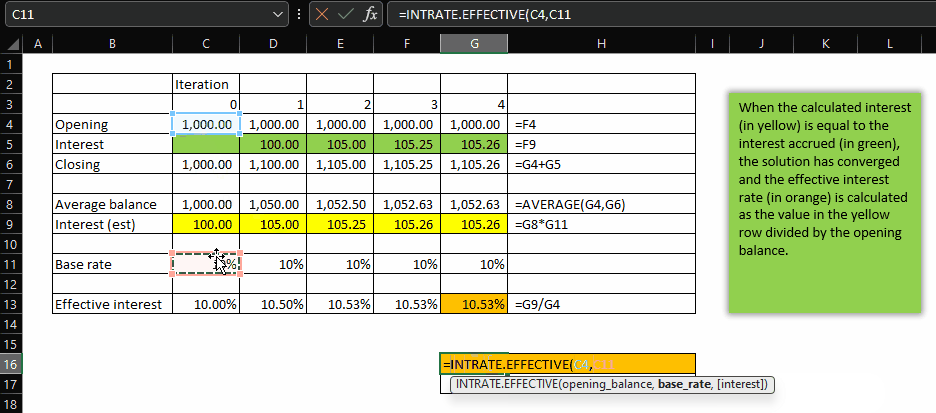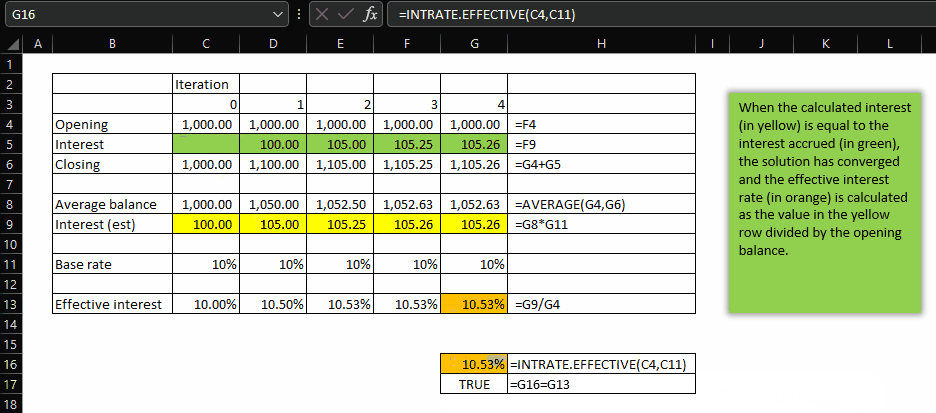
Let’s break it down

Looking again at the definition:

=LAMBDA(opening_balance, base_rate, [interest],
    LET(
        _int, IF(ISOMITTED(interest), 0, interest),
        _new_close, opening_balance + _int,
        _avg_balance, AVERAGE(opening_balance, _new_close),
        _new_int, _avg_balance * base_rate,
        _effective_rate, IF(
            ROUND(_new_int, 2) = ROUND(_int, 2),
            _new_int / opening_balance,
            INTRATE.EFFECTIVE(opening_balance,base_rate,_new_int)
        ),
        _effective_rate
    )
)

As usual, we’re using LET to define some names to use in the calculations. My convention is to prefix variables with an underscore so they are easily distinguishable from parameters. 

• _int – here we check if a value has been provided for the interest parameter. If it hasn’t we assign 0 (zero) to _int, otherwise we assign whatever value was provided. When calling from the spreadsheet (i.e. not from a recursion call), this will always produce 0, which is equivalent to the 0-th iteration shown at the top of the gif above.
• _new_close – we calculate the closing balance during this iteration as being the opening balance plus the value of _int just calculated. In the 0-th iteration, this will simply be equal to the opening balance.
• _avg_balance – in this simple example lambda, the assumption is that the interest was applied to the opening balance halfway through a period, so the calculation of “interest upon interest” is only based on the average of the opening and closing balance. In your calculations, this may be overly simplified and, should you choose to use this lambda, you may need to modify how this works accordingly.
• _new_int – here we calculate the interest for this iteration, which is just the average balance multiplied by the base rate.
• _effective_rate – here we check if the interest value _new_int, rounded to 2 decimal places, is equal to the same rounding of _int, which is to say: is _new_int, on any iteration >0, the same as the interest calculated on the previous iteration (which is provided to the interest parameter). If they are the same, we say that the iterations have converged and we assign the value _new_int / opening balance to the _effective_rate variable and this is then used as the exit point for the function. If those two rounded numbers are not the same, then the iterations have not converged, and we call INTRATE.EFFECTIVE, with the same opening balance and base rate, only this time we pass the calculated _new_int from this iteration as the interest parameter for the next. The net effect of calling the function from within itself is to move rightward across the columnar list of iterations shown in the gif above. Eventually, the IF comparison returns TRUE and the function exits with the calculation shown.

In summary

We saw how to calculate effective interest rate in Excel without iterative calculation using a recursive lambda function. 

By using an appropriate exit strategy (i.e. rounded interest this iteration is equal to rounded interest from the previous iteration), we avoid infinite recursion.

Again, this function is based on simple assumptions and my intent here was to show the technique rather than provide a bulletproof function that can be used in many real-world scenarios.