Excel LAMBDA: Introducing the LAMB namespace

Posted on by OP

The gist for this namespace can be found here. 

The goals

When I was first learning about LAMBDA in Excel, I wrote some functions to calculate outlier tests against a column of data. 

The main function – OUTLIER.TESTS – allowed us to write a single formula, apply a collection of transformations, and run a standard deviation test against each of the transformations of the variable.

It was really exciting to me that we could now do this so easily in Excel.

You can see how it works below.

Each test returns three columns indicating which rows in the transformed data were either Low or High outliers according to the standard deviation test performed against the transformed variable.

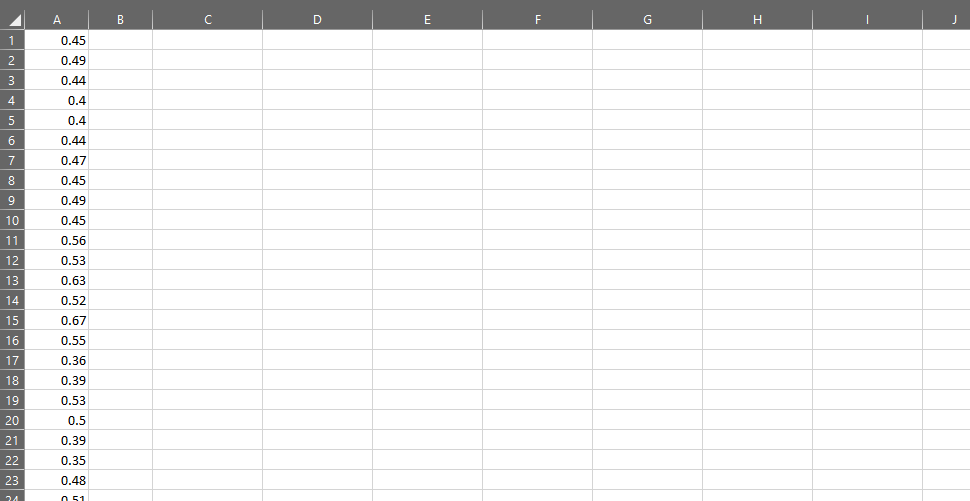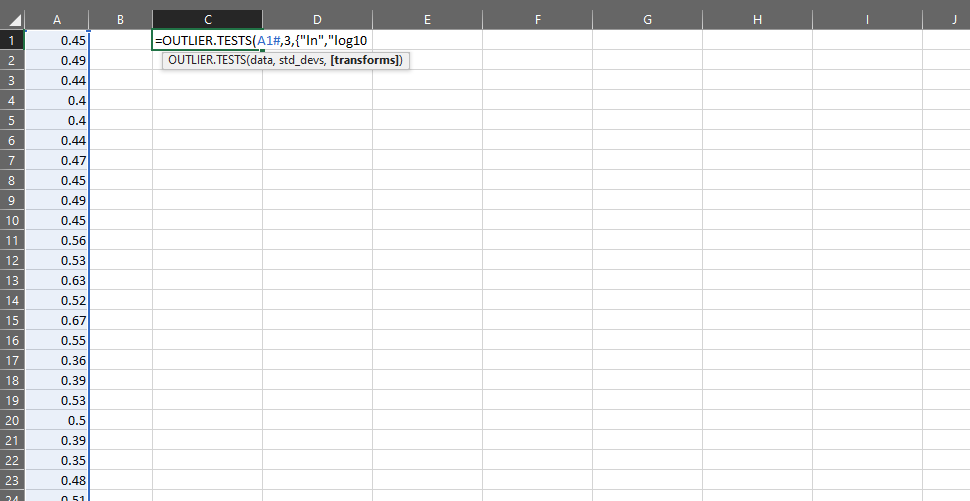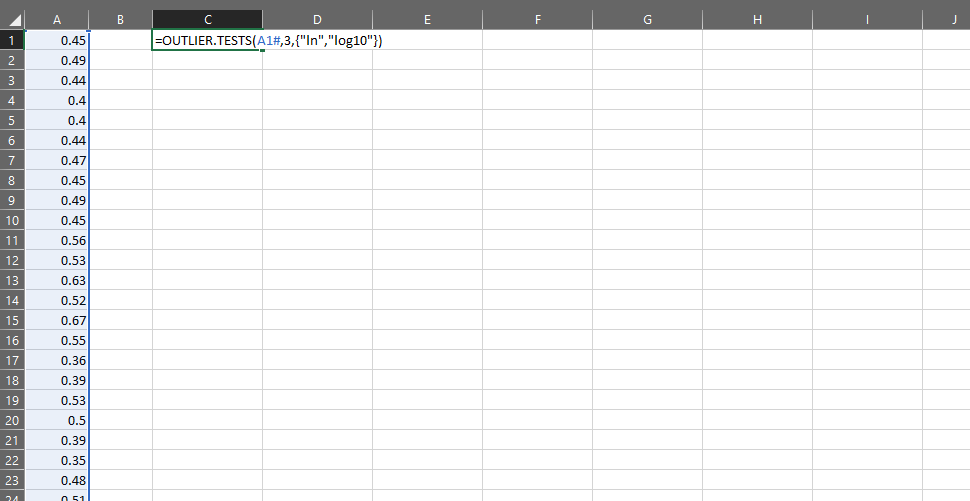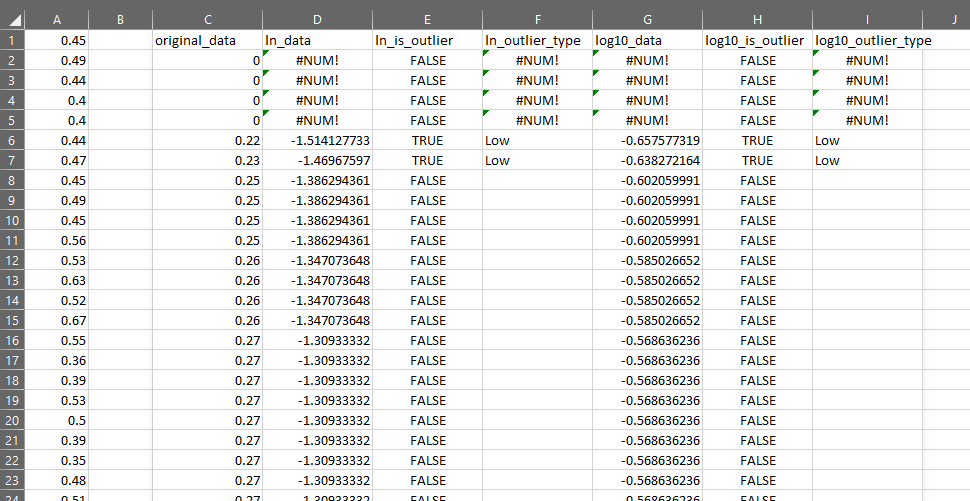
You can read the details about how it works here.

I still think this function is useful, but it has some issues which I want to correct. 

  1. It’s very slow. See how long it takes after finishing the formula before it returns the data?
  2. The transformations in must be typed exactly as they are specified in the code for the lambda – if you make a typo in one of the transformation names, the function won’t work.
  3. The transformations that can be used are hard-coded in the lambda. It’s not easy to add new transformations.

Since then, I’ve learned a few things about lambda and functional programming in Excel which I think will help improve this outlier.tests function.

This exercise will focus on the creation of two namespaces to support the changes, which I will cover in two blog posts:

  1. LAMB – this will be a namespace for functions that will support the second namespace. Eventually I plan for this namespace to contain many other general-purpose functions as well.
  2. OUTLIERS – this is where the main testing functions will be. 

This post will cover the first namespace – LAMB, and the goals will be to:

1. Create a function for easily constructing an array of functions which can be passed as a parameter to another function
2. Build a small library of lambdas that can be used to transform a column of data (such as might be needed in correcting skew)
3. Create a way to apply an array of functions to some data

1. Create a function for creating an array of functions

If you decide to import the gist, please note that it should be imported to a new namespace called LAMB. For a quick primer on namespaces, read this.

/*****************************************************************************************
******************************************************************************************
Array of functions
******************************************************************************************

Allows for creation of an array of functions which can be passed as a parameter to another function

Original credit to: Travis Boulden

https://www.mrexcel.com/board/threads/ifanyof.1184234/

Function named "either" on that page

In the code below, I have simplified slightly to use VSTACK instead of CHOOSE
and SUM instead of REDUCE to calculate the count of not-omitted functions

e.g. Apply the SQRT, LN and LOG_10 transformations to the wine vector:

=LAMB.TRANSFORM(wine, LAMB.FUNCS(LAMB.SQRT, LAMB.LN, LAMB.LOG_10))

Issue here is if we provide fn_1, don't provide fn_2, then provide fn_3, it will try to return
an array containing fn_1 and fn_2
*/
FUNCS =LAMBDA(
    fn_1,[fn_2],[fn_3],[fn_4],[fn_5],
    [fn_6],[fn_7],[fn_8],[fn_9],[fn_10],
    LET(

      //An array indicating which functions are omitted
      omitted_fns,
        VSTACK(
          ISOMITTED(fn_1),ISOMITTED(fn_2),
          ISOMITTED(fn_3),ISOMITTED(fn_4),
          ISOMITTED(fn_5),ISOMITTED(fn_6),
          ISOMITTED(fn_7),ISOMITTED(fn_8),
          ISOMITTED(fn_9),ISOMITTED(fn_10)
        ),

      //count of the not omitted functions
      fn_ct,SUM(--NOT(omitted_fns)),

      //return the first fn_ct functions in an array
      fns,
        CHOOSE(SEQUENCE(fn_ct),
          fn_1,fn_2,fn_3,fn_4,fn_5,
          fn_6,fn_7,fn_8,fn_9,fn_10
        ),
      fns
    )
);

This function takes 1 required parameter and 9 optional parameters.

Each parameter is a LAMBDA function. 

The purpose of this function is to combine up to 10 lambda functions into an array and return the array of functions.

The return value (an array of functions) can then be passed as a single parameter to another function which can use those functions in that array in its own processing. 

We use LET to define some variables:

  • omitted_fns – this uses VSTACK to stack the boolean results from the ISOMITTED function having been called on each of the parameters. If we pass two functions – in parameters fn_1 and fn_2, then omitted_fns = {FALSE, FALSE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE}
  • fn_ct – here we convert omitted_fns to its opposite using NOT, giving us in the example above NOT(omitted_fns) = {TRUE, TRUE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE}. If we then applying the double-unary operator (two minus signs), we convert that array to –NOT(omitted_fns) = {1,1,0,0,0,0,0,0,0,0}. Summing this final array gives us a count of 2. So fn_ct is the count of non-omitted functions.
  • fns – we use CHOOSE(SEQUENCE(fn_ct),… with the list of parameter names to return the first fn_ct parameters from the full list of parameters.
    • There is a weakness to this approach in that if, for example, fn_1 is provided, then fn_2 is omitted, but fn_3 is provided, and the remainder are omitted, then the count is 2, but the function expects the arguments to be passed to parameters fn_1 and fn_2. This will produce a #VALUE! error. It’s a weakness to be aware of but I think it’s enough to know that the function-parameters must be front-loaded into LAMB.FUNCS; i.e. you should take care not to have any gaps between provided functions.

There’s no sensible visual example for this function since we can’t actually display a function in a spreadsheet cell.

That said, we can create an array of two simple functions like this:

=LAMB.FUNCS(LAMBDA(a,a+1),LAMBDA(a,a+2))

You can see that each parameter is a LAMBDA function.

But remember, if we have a named lambda (i.e. it’s saved in the Name Manager), then we can just pass the name in place of the LAMBDA(…, …) definition.

So, suppose:

ADD_ONE = LAMBDA(a,a+1);
ADD_TWO = LAMBDA(a,a+2);

Then the following is equivalent to the code above:

=LAMB.FUNCS(ADD_ONE, ADD_TWO)

It returns an array containing the lambdas ADD_ONE and ADD_TWO.

That’s our first goal complete. We now have a function that will allow us to create an array of functions. 

2. Library of transformations

Now that we have a function that will create an array of functions, we need some functions to put into that array!

Remember: all the functions mentioned in this post are in the LAMB namespace, so if you see LAMB. before the function name, that’s why. 

/*****************************************************************************************
******************************************************************************************
Library of transformation lambdas
******************************************************************************************
Author: OWEN PRICE
Date: 2022-08-27

Examples of simple vector transforms that can be applied sequentially using LAMB.TRANSFORM
*/

//Wraps the SQRT function as a lambda so it can be passed around other functions
SQRT = LAMBDA(vector, SQRT(vector));

//Wraps the LN function as a lambda so it can be passed around other functions
LN = LAMBDA(vector, LN(vector));

/*
Returns a lambda of the LOG at the specified base

The returned lambda can then be passed to other functions

To create a "log base 10" function:
=outlier.log(10)

To use that function with a vector v:
=outlier.log(10)(v)
*/
LOG = LAMBDA(base, LAMBDA(vector, LOG(vector, base)));

//For simplicity, create a lambda function for applying the log10 transform to a vector
LOG_10 = LAMBDA(vector, LAMB.LOG(10)(vector));


//Returns a lambda function that raises a vector to the given power
POWER = LAMBDA(exponent, LAMBDA(vector, POWER(vector, exponent)));

RECIPROCAL = LAMBDA(vector, LAMB.POWER(-1)(vector));

RECIPROCAL_SQ = LAMBDA(vector, LAMB.POWER(-2)(vector));

CUBEROOT = LAMBDA(vector, LAMB.POWER(1/3)(vector));

The functions listed above are very simple. As a summary, they are lambda versions of the following transformations:

  • SQRT – the square root transform
  • LN – the natural logarithm
  • LOG (base) – the logarithm with the given base
  • LOG(10) – which is a special case of LOG(base)
  • POWER(exp) – the transform that raises a number using the given exponent
  • RECIPROCAL – uses the POWER lambda, since the reciprocal of a vector that vector raised to the power -1
  • RECIPROCAL_SQ – which again uses the POWER lambda, this time with exponent -2
  • CUBEROOT – POWER with exponent 1/3

This is just a small collection of common vector transforms that can be used in cases where a variable may appear skewed.

The important thing to remember here is that by defining our transforms in this way, we can easily add new transforms that can be arbitrarily complex. 

Most of the functions above should be self-explanatory, but let’s look quickly at LAMB.LOG:

LOG = LAMBDA(base, LAMBDA(vector, LOG(vector, base)));

You can see that it’s very simple.

It has one parameter – base, which is an integer to be passed into Excel’s native LOG function.

Suppose we pass the value 10 into this lambda:

=LAMB.LOG(10)

The return value for this function call is a lambda function:

LAMBDA(vector, LOG(vector, 10))

The lambda produced has itself exactly one parameter – vector.

If we want to apply the log base 10 transform to a vector v, then we can use this returned lambda like this:

=LAMBDA(vector, LOG(vector, 10))(v)

Or we can just do this:

=LAMB.LOG(10)(v)

By making the outer lambda a one-parameter function that returns a one-parameter function, we are using a technique called currying to encapsulate each parameter of the entire operation into a function of its own. 

In this way, we can pass one parameter at a time and move the function between other processing steps between parameter assignments.

In this example, using this technique allows us to use the function returned by LAMB.LOG(10) as the calculation inside the LAMB.LOG_TEN function.

LOG = LAMBDA(base, LAMBDA(vector, LOG(vector, base)));
LOG_10 = LAMBDA(vector, LAMB.LOG(10)(vector));

You can also see the same technique being used to define the reciprocal, square reciprocal and cube-root functions, which are special cases of the POWER function:

POWER = LAMBDA(exponent, LAMBDA(vector, POWER(vector, exponent)));
RECIPROCAL = LAMBDA(vector, LAMB.POWER(-1)(vector));
RECIPROCAL_SQ = LAMBDA(vector, LAMB.POWER(-2)(vector));
CUBEROOT = LAMBDA(vector, LAMB.POWER(1/3)(vector));

Still here? Great! We’re getting there!

Now we’ve got a function that creates an array of functions, and we’ve got some functions to go into that function, we can create an array of transformations to apply to a vector.

Remembering that we can pass a lambda function as a parameter to another function, we can create an array of functions that contains the LN, the SQRT and the RECIPROCAL transforms by doing this:

=LAMB.FUNCS(LAMB.LN, LAMB.SQRT, LAMB.RECIPROCAL)

3. Create a way to apply an array of functions to some data

OK, so now we’ve created a way to store an array of functions.

We’ve also created some functions to go into such an array.

Why though? Well, all of this is leading to being able to do this:

Here’s the code for LAMB.TRANSFORM:

/*
Author: OWEN PRICE
Date: 2022-08-27

Used to transform a vector once for each transformation function in transform_fns

e.g. transform the 'wine' vector using SQRT, LN and LOG10

=LAMB.TRANSFORM(vector, LAMB.FUNCS(LAMB.SQRT, LAMB.LN, LAMB.LOG_10))

*/
TRANSFORM =LAMBDA(vector,transform_fns,
  REDUCE(vector,transform_fns,LAMBDA(a,b,HSTACK(a,b(vector))))
);

This function takes two parameters:

  1. vector – is a column of data. In the example above, I’m using a named range called ‘wine’.
  2. transform_fns – is an array of transformation functions. This is created using LAMB.FUNCS as described above.

The great thing about this is that the exact transformations we want to use each time we call this LAMB.TRANSFORM function are not known until we need to use them.

We simply pass it an array of functions – each of which is defined in any way we choose – and as long as each of those functions in that array accept one parameter only (by judicious use of currying), then LAMB.TRANSFORM will apply each function to the vector and return an array that has one column for the original vector followed by one column for each transformation function applied to that vector.

The calculation is simple:

REDUCE(vector,transform_fns,LAMBDA(a,b,HSTACK(a,b(vector))))

To put that into words:

  • Take the vector that was passed into LAMB.TRANSFORM and use it as the initial_value for the REDUCE function.
  • Scan through the array of functions in the transform_fns array (remember, this was created with LAMB.FUNCS).
  • At each element of the transform_fns array, HSTACK the result of the previous iteration – a – with the result of applying to the vector the function represented by the current row in the transform_fns array, which is referenced using the parameter b. That’s what b(vector) is doing.

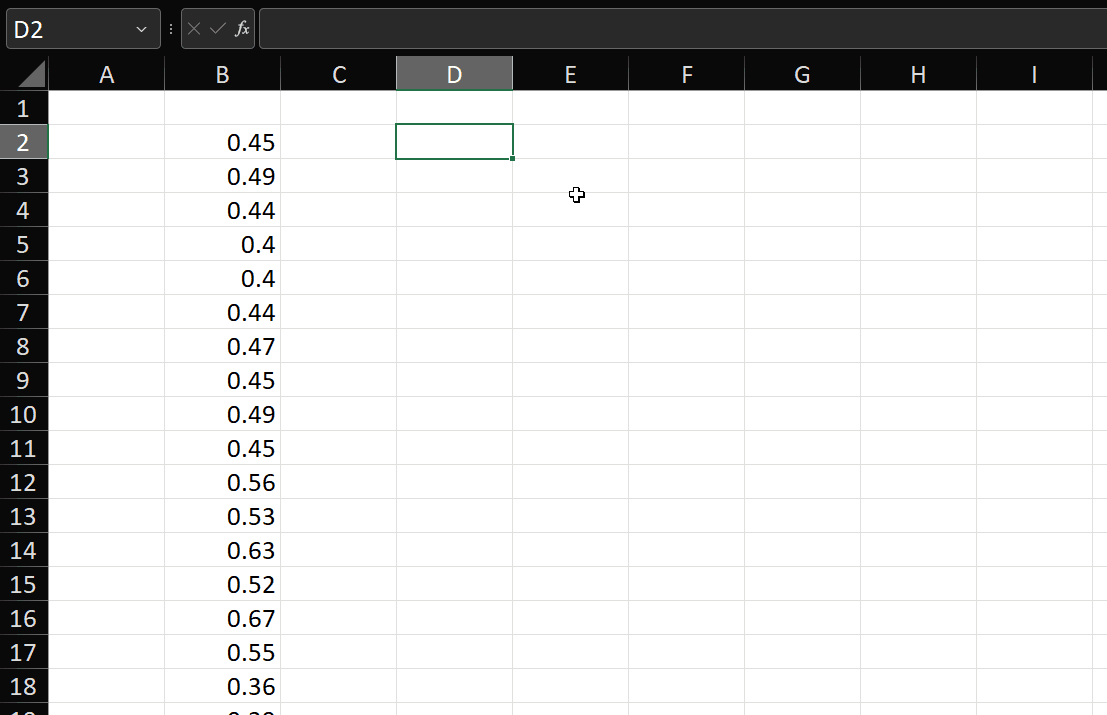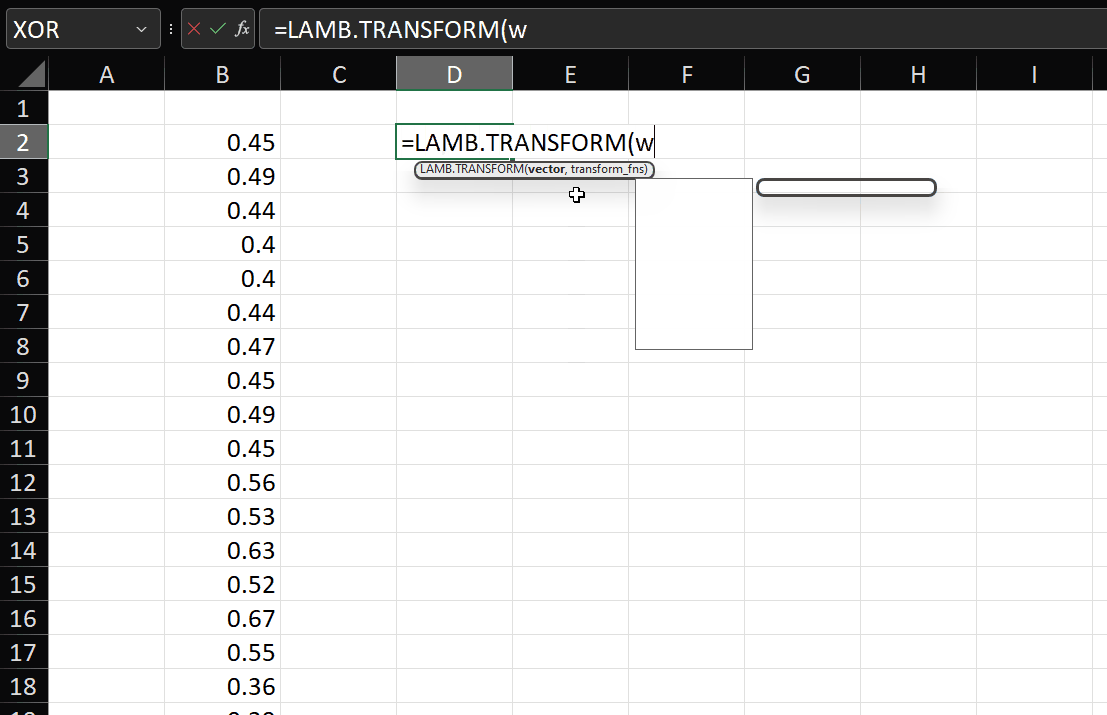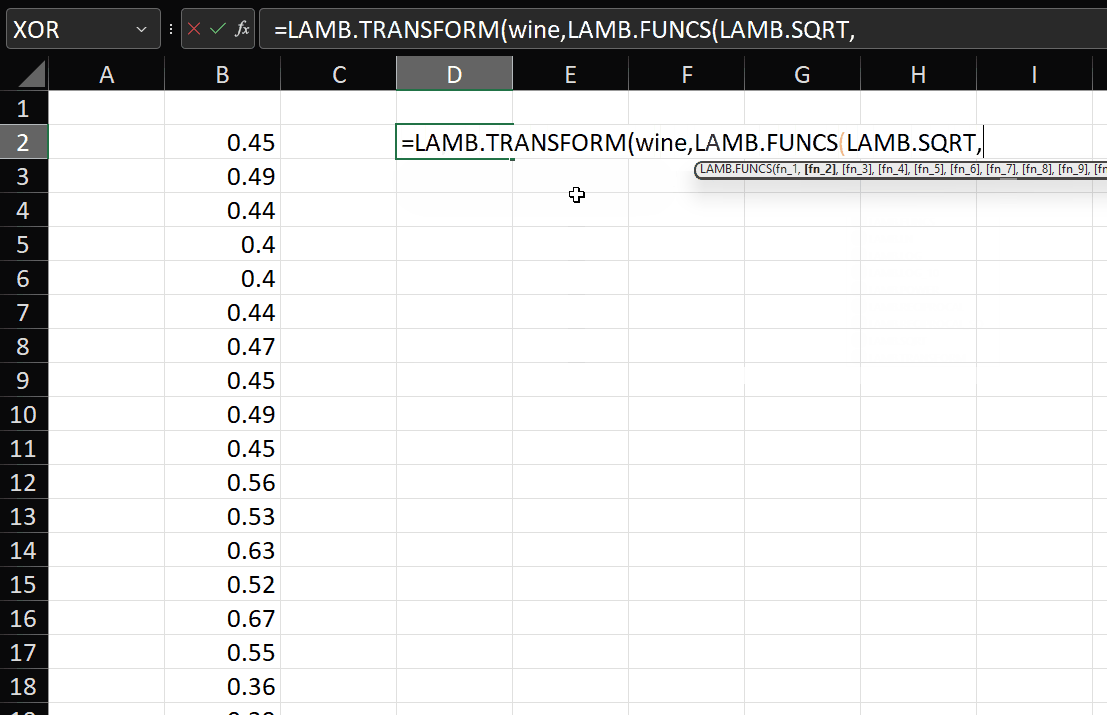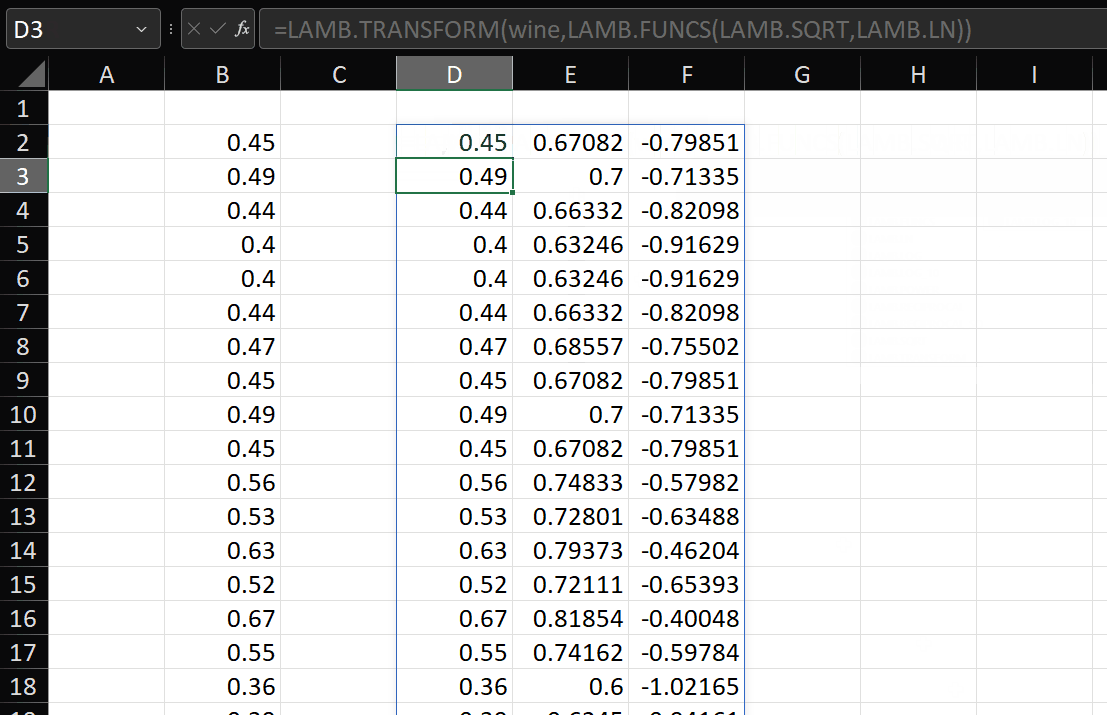
So, if we call the function as shown in the gif above:

=LAMB.TRANSFORM(wine,LAMB.FUNCS(LAMB.SQRT,LAMB.LN))

Then:

  • vector = wine (which is the data in column B)
  • the array of functions contains 2 elements – the LAMB.SQRT function, and the LAMB.LN function
  • When the REDUCE scan begins, the initial_value is the data in the vector parameter – ‘wine’.
  • The LAMBDA function within REDUCE assigns this initial value to the accumulator – a – and the value in the current row of the transform_fns array to the other parameter – b. Remember, each value assigned to b is a function.
  • On iteration 1, initial_value = vector = wine = a and b = LAMB.SQRT, therefore b(vector) = LAMB.SQRT(wine) and the result of the first iteration is HSTACK(wine,LAMB.SQRT(wine))
  • The result of iteration 1 is then assigned to a for iteration 2:
    • a = HSTACK(wine, LAMB.SQRT(wine)), and
    • b = LAMB.LN, therefore b(vector) = LAMB.LN(wine) and the result of the second iteration is HSTACK(a, LAMB.LN(wine)) = HSTACK(HSTACK(wine, LAMB.SQRT(wine)), LAMB.LN(wine))

Since there are only two functions, the result of LAMB.TRANSFORM is just the result of the 2nd iteration (because that’s how REDUCE works):

=LAMB.TRANSFORM(wine,LAMB.FUNCS(LAMB.SQRT,LAMB.LN)) = HSTACK(HSTACK(wine, LAMB.SQRT(wine)), LAMB.LN(wine))

This all might seem pretty complicated, but by organizing the transform function in this way, we don’t have to write out HSTACK(HSTACK(HSTACK(… in an increasingly complex formula to get the result we want each time we add a new transform function. We simply pass the vector into the LAMB.TRANSFORM function once, then pass that vector into each of those one-parameter functions we stored in the array created by LAMB.FUNCS.

Adding a new transform to this framework is now trivially easy.

We can have between 1 and 10 transforms applied at once.

And we can be confident that the exact calculation being performed by each of the transforms is the same each time we use it. No more googling “cube root function Excel”.

In summary

This was the first part in a two-part blog post that aims to simplify and modularize some lambda for handling numerical outliers.

In this post, we saw how to create an array of functions using the techniques in LAMB.FUNCS.

We saw how to create a small library of simple transformation lambdas.

We saw how to use currying to force a lambda function to be a one-parameter lambda. 

We saw how to use the REDUCE function to apply an array of functions to a vector using LAMB.TRANSFORM. 

In the next post, I will put all of this to use in the functions in the OUTLIER namespace. 

Leave a Reply

Your email address will not be published. Required fields are marked *

You may use these HTML tags and attributes:

<a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>