In this post you’ll learn to unfold a list from a value with a recursion wrapper called LIST.UNFOLD.
INTRODUCTION
In Excel as in many other languages, we can use REDUCE to reduce (or fold) a list into a single value. We iterate over the list, and at each element apply a function. The result of that function becomes what’s known as an accumulator. This accumulator created from applying the function to one element is passed as an argument to the same function when it is applied to the next element. This continues until the last element of the list is reached, at which point the accumulator becomes the result.
So, with REDUCE, we can create a single value from a list and a function.
In some languages this operation is known as “folding”. In fact, I talked about that in an earlier post. It turns out that in several functional programming languages have built-in capability to do the opposite of the reduce (or fold) operation.
Let’s look at List.unfold from F#. Here’s the example from the documentation:
|> List.unfold (fun state -> if state > 100 then None else Some (state, state * 2))
Both Some and None are part of what’s known as an Option type in F#. They are used to safely handle values that might or might not exist. When the if statement returns true, i.e. when state is greater than 100, the return of None is an error-safe way to indicate that there are no more values to add to the list. This is essentially the exit condition to tell List.unfold to stop. If state is less than or equal to 100, Some (state, state * 2) creates a tuple whose first element is the next element to be added to the list. The second element is the new value of state to pass to the next iteration of the generator function. So, this is a concise way of using recursion to generate a list and one of the many reasons why F# is a great language!
Reading this you may be thinking… hey, is that why we have List.Generate in Power Query?
Yes. Yes, it is.
In fact, my observation is that List.Generate encapsulates the functionality of List.unfold and adds additional functionality to handle common data mashup use cases that might be needed in the realms of Excel, Power BI et al.
Anyway, we’re getting off track! Let’s look at LIST.UNFOLD as an Excel LAMBDA function!
LIST.UNFOLD
Here’s the code for LIST.UNFOLD:
LIST.UNFOLD = LAMBDA(generator_function,
LAMBDA(value,
LET(
_result, generator_function(value),
IF(ISNA(@TAKE(_result,-1, 1)), value, LIST.UNFOLD(generator_function)(_result))
)
)
);
Looks simple, right? And it is! I’ll break it down for you in a minute, but let’s talk about the signature. There are two required (and curried) parameters. The reason for that will become clear shortly.
- generator_function – this is the function that will take the current state of the list and produce a new value to be added. This function can be very simple or incredibly complex. The requirement placed on this function is that it has one parameter. There is no requirement on the type of that parameter.
- value – this is the current state of the list. When we call LIST.UNFOLD, we’ll give this inner lambda a seed value to get started on, and as the function recurses, the list being created will be passed into this parameter.
Here’s an example of how LIST.UNFOLD works:
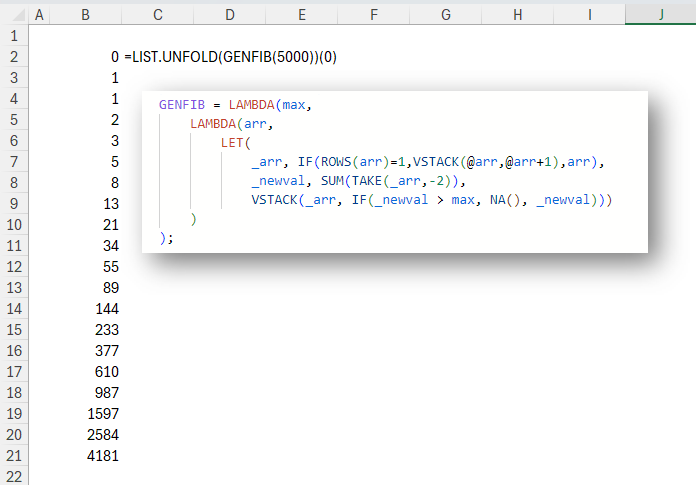
GENFIB is a general implementation of a Fibonacci-like sequence. This function calculates the new value as the sum of the previous two values. It then stacks the new value underneath the previous values. Here’s the code for GENFIB:
GENFIB = LAMBDA(max,
LAMBDA(arr,
LET(
_arr, IF(ROWS(arr)=1,VSTACK(@arr,@arr+1),arr),
_newval, SUM(TAKE(_arr,-2)),
VSTACK(_arr, IF(_newval > max, NA(), _newval)))
)
);
The important thing here is that we can configure the exit condition by passing the first parameter as the value which will serve as an exit condition for the function. So this:
GENFIB(5000)
Returns this:
LAMBDA(arr,
LET(
_arr, IF(ROWS(arr)=1,VSTACK(@arr,@arr+1),arr),
_newval, SUM(TAKE(_arr,-2)),
VSTACK(_arr, IF(_newval > 5000, NA(), _newval)))
)
Now we can see that if the _newval (state) is greater than 5000, the function will stack NA() to the bottom of the list. This is a design decision I’ve made for LIST.UNFOLD. When LIST.UNFOLD encounters an NA() at the bottom of the list, it will stop. So any function passed to LIST.UNFOLD must use this fact to control the exit condition.
One thing to note about GENFIB itself is that it is not a recursive function. All it does is calculate one value. The recursion is handled by LIST.UNFOLD. This is a way to remove the difficult part of the programming from the logic of the sequence and re-use it whenever it’s needed.
Without further ado, let’s take a close look at how LIST.UNFOLD works!
BREAKDOWN
For reference, here’s the code for LIST.UNFOLD again. I’ve included the code for GENFIB as it may be helpful in the following explanation.
LIST.UNFOLD = LAMBDA(generator_function,
LAMBDA(value,
LET(
_result, generator_function(value),
IF(ISNA(@TAKE(_result,-1, 1)), value, LIST.UNFOLD(generator_function)(_result))
)
)
);
GENFIB = LAMBDA(max,
LAMBDA(arr,
LET(
_arr, IF(ROWS(arr)=1,VSTACK(@arr,@arr+1),arr),
_newval, SUM(TAKE(_arr,-2)),
VSTACK(_arr, IF(_newval > max, NA(), _newval)))
)
);
So, we pass a generator_function into the outer lambda of LIST.UNFOLD. An example is GENFIB(5000) which returns the function discussed above:
=LIST.UNFOLD(GENFIB(5000))
That returns this inner function:
LAMBDA(value,
LET(
_result, generator_function(value),
IF(ISNA(@TAKE(_result,-1, 1)), value, LIST.UNFOLD(generator_function)(_result))
)
)
Where generator_function is:
LAMBDA(arr,
LET(
_arr, IF(ROWS(arr)=1,VSTACK(@arr,@arr+1),arr),
_newval, SUM(TAKE(_arr,-2)),
VSTACK(_arr, IF(_newval > 5000, NA(), _newval)))
)
When you expand all of this, that small line has actually created this function!
UNFOLD.GENFIB5000 =
LAMBDA(value,
LET(
generator_function,
LAMBDA(arr,
LET(
_arr, IF(ROWS(arr)=1,VSTACK(@arr,@arr+1),arr),
_newval, SUM(TAKE(_arr,-2)),
VSTACK(_arr, IF(_newval > 5000, NA(), _newval)))
),
_result, generator_function(value),
IF(ISNA(@TAKE(_result,-1, 1)), value, LIST.UNFOLD(generator_function)(_result))
)
);
Which is part of the reason I wanted to put the recursion logic inside LIST.UNFOLD. Anyway, let’s get back on track. Here’s LIST.UNFOLD again.
LIST.UNFOLD = LAMBDA(generator_function,
LAMBDA(value,
LET(
_result, generator_function(value),
IF(ISNA(@TAKE(_result,-1, 1)), value, LIST.UNFOLD(generator_function)(_result))
)
)
);
_result is the result of whatever generator_function produces when we give it value.
An example:
=LIST.UNFOLD(GENFIB(5000))(0)
This function passes 0 into the generator_function GENFIB(5000).
LAMBDA(arr,
LET(
_arr, IF(ROWS(arr)=1,VSTACK(@arr,@arr+1),arr),
_newval, SUM(TAKE(_arr,-2)),
VSTACK(_arr, IF(_newval > 5000, NA(), _newval)))
)
So 0 is arr. And since ROWS(0)=1, this GENFIB function assigns VSTACK(0, 0+1) to _arr. This is important because a Fibonacci-like calculation requires two values to calculate the next value. The design choice here is to say if this function has only been given one value, then we’ll just put the next integer after it and continue as if there were two values in the array originally.
_newval is then the sum of those two values. Finally, check if _newval is greater than 5000 and if it isn’t, return _arr with _newval stacked underneath.
This return value is, as mentioned, assigned to _result in LIST.UNFOLD:
LIST.UNFOLD = LAMBDA(generator_function,
LAMBDA(value,
LET(
_result, generator_function(value),
IF(ISNA(@TAKE(_result,-1, 1)), value, LIST.UNFOLD(generator_function)(_result))
)
)
);
Passing 0 to value as we did means that _result will be {0; 1; 1} after the first iteration.
The next line of LIST.UNFOLD first checks if the last row in _result is NA(). If it is, LIST.UNFOLD exits and returns value (i.e. the state of the list after the previous iteration). If the value of the last row is not NA(), LIST.UNFOLD is called again, but this time _result is the new argument to value.
When value={0; 1; 1} in GENFIB, ROWS({0; 1; 1})=3, so _arr=arr and _newval=SUM(TAKE({0; 1; 1},-2))=SUM({1; 1})=2. Further, _newval is not greater than 5000, so the return value of the generator function is now VSTACK({0; 1; 1}, 2)={0; 1; 1; 2}, which becomes _result in UNFOLD.LIST, and so on and so forth until the exit condition is met!
The recursion, which is fairly standard behavior across the family of functions that produce sequences, is always handled in the same way, and so has been abstracted into the LIST.UNFOLD function. The real logic of what the syntax is is embedded in the generator function, which as I mentioned before, can be as simple or as complex as you like. Here are a few examples:
GEOMETRIC = LAMBDA(common_ratio, break_at,
LAMBDA(x,
LET(
_newval, @TAKE(x,-1)*common_ratio,
VSTACK(x, IF(OR(AND(common_ratio<1,_newval<break_at),
AND(common_ratio>=1,_newval>break_at)), NA(), _newval))))
);
POWERSEQ = LAMBDA(power,ceiling,
LAMBDA(x, LET(_newval, @TAKE(x,-1)^power, VSTACK(x,IF(_newval > ceiling, NA(), _newval))))
);
GENFIB = LAMBDA(max,
LAMBDA(arr,
LET(
_arr, IF(ROWS(arr)=1,VSTACK(@arr,@arr+1),arr),
_newval, SUM(TAKE(_arr,-2)),
VSTACK(_arr, IF(_newval > max, NA(), _newval)))
)
);
CATALAN =LAMBDA(max, mode,
LAMBDA(
arr,
LET(
_n, TAKE(arr,-1,-1),
_Cn, TAKE(arr,-1,1),
_newVal, _Cn * 2 * (2*_n + 1) / (_n + 2),
VSTACK(arr, IF(
IF(mode=0,_newVal,_n+2) > max
, NA(), HSTACK(_newVal, _n + 1)))
)
)
);
These are somewhat trivial examples since, according to my 8-step process for writing recursive functions in Excel, they probably aren’t necessary.
However, I’d just like to remind you that recursion is either necessary for the program or for the programmer. If it makes the programming easier to understand, then use it!
SUMMARY
In this post we saw how to unfold a list with this new function – LIST.UNFOLD.
LIST.UNFOLD is a recursion wrapper for the family of functions that produce complex sequences. Like List.Generate in Power Query, and List.unfold in F#, we can pass a generator function to LIST.UNFOLD along with a seed value, to create a new list, making it equivalent to the reverse of REDUCE!
I hope you enjoyed reading about it and that it sparked some ideas. Let me know in the comments if you have any questions!